Вопрос 38: Технологии Data Mining. Алгоритмы Data Mining

Data Mining – это процесс обнаружения в "сырых" данных ранее неизвестных нетривиальных практически полезных и доступных интерпретации знаний, необходимых для принятия решений в различных сферах человеческой деятельности.

В Data Mining для представления знаний служат модели, вид которых зависит от методов их создания, наиболее распространенными являются: правила, деревья решений, кластеры и математические функции.

Задачи, решаемые методами Data Mining:

1. Классификация – это отнесение объектов (наблюдений, событий) к одному из заранее известных классов.
2. Регрессия, в том числе задачи прогнозирования. Установление зависимости непрерывных выходных от входных переменных.
3. Кластеризация – это группировка объектов (наблюдений, событий) на основе данных (свойств), описывающих сущность этих объектов. Объекты внутри кластера должны быть "похожими" друг на друга и отличаться от объектов, вошедших в другие кластеры. Чем больше похожи объекты внутри кластера и чем больше отличий между кластерами, тем точнее кластеризация.
4. Ассоциация – выявление закономерностей между связанными событиями. Примером такой закономерности служит правило, указывающее, что из события X следует событие Y. Такие правила называются ассоциативными. Впервые эта задача была предложена для нахождения типичных шаблонов покупок, совершаемых в супермаркетах, поэтому иногда ее еще называют анализом рыночной корзины (market basket analysis).
5. Последовательные шаблоны – установление закономерностей между связанными во времени событиями, т.е. обнаружение зависимости, что если произойдет событие X, то спустя заданное время произойдет событие Y.
6. Анализ отклонений – выявление наиболее нехарактерных шаблонов.

Перечисленные задачи по назначению делятся на описательные и предсказательные:

• Описательные (descriptive) задачи уделяют внимание улучшению понимания анализируемых данных. Ключевой момент в таких моделях — легкость и прозрачность результатов для восприятия человеком. Возможно, обнаруженные закономерности будут специфической чертой именно конкретных исследуемых данных и больше нигде не встретятся, но это все равно может быть полезно и потому должно быть известно. К такому виду задач относятся кластеризация и поиск ассоциативных правил.

• Решение предсказательных (predictive) задач разбивается на два этапа. На первом этапе на основании набора данных с известными результатами строится модель. На втором этапе она используется для предсказания результатов на основании новых наборов данных. При этом, естественно, требуется, чтобы построенные модели работали максимально точно. К данному виду задач относят задачи классификации и регрессии. Сюда можно отнести и задачу поиска ассоциативных правил, если результаты ее решения могут быть использованы для предсказания появления некоторых событий.

По способам решения задачи разделяют на:

• supervised learning (обучение с учителем)
• unsupervised learning (обучение без учителя).

Такое название произошло от термина Machine Learning (машинное обучение), часто используемого в англоязычной литературе и обозначающего все технологии Data Mining.

В случае supervised learning задача анализа данных решается в несколько этапов. Сначала с помощью какого-либо алгоритма Data Mining строится модель анализируемых данных – классификатор. Затем классификатор подвергается обучению. Другими словами, проверяется качество его работы и, если оно неудовлетворительно, происходит дополнительное обучение классификатора. Так продолжается до тех пор, пока не будет достигнут требуемый уровень качества или не станет ясно, что выбранный алгоритм не работает корректно с данными, либо же сами данные не имеют структуры, которую можно выявить. К этому типу задач относят задачи классификации и регрессии.

Unsupervised learning объединяет задачи, выявляющие описательные модели, например закономерности в покупках, совершаемых клиентами большого магазина. Очевидно, что если эти закономерности есть, то модель должна их представить и неуместно говорить об ее обучении. Отсюда и название — unsupervised learning. Достоинством таких задач является возможность их решения без каких-либо предварительных знаний об анализируемых данных. К ним относятся кластеризация и поиск ассоциативных правил.

Методы Data Mining

1. Базовые методы (методы основанные на переборе)
2. Нечеткая логика (отображение на формальном языке анализируемых данных и последующий анализ полученной модели)
3. Генетические алгоритмы (методы оптимизации, способные решать задачи различных типов и степени сложности)
4. Нейронные сети (Алгоритмы основанные на биологической аналогии с мозгом человека)

Процесс обнаружения знаний:

1. Понимание и формулировка задачи анализа.
2. Подготовка данных для автоматизированного анализа (препроцессинг).
3. Применение методов Data Mining и построение моделей.
4. Проверка построенных моделей.
5. Интерпретация моделей человеком.

Алгоритмы

Классификация и регресия

Модели

1. Правила классификации
2. Деревья решений
3. Математические функции

Алгоритмы

1. Методы построения правил классификации
   1. Алгоритм построения 1-правил
   2. Метод Naive Bayes
2. Методы построения деревьев решений
   1. Методика "разделяй и властвуй"
   2. Алгоритм покрытия
3. Методы построения математических функций
   1. Линейные методы. Метод наименьших квадратов
   2. Нелинейные методы
   3. Support Vector Machines (SVM)
4. Карты Кохонена

Алгоритм построения 1-правил

Алгоритм требуется для формирования элементарных правил для классификации объекта. Он строит правила по значению одной независимой переменной, поэтому и называется 1-правило или 1R(rule)-алгоритм.

Идея алгоритма состоит в том, что для любого возможного значения каждой независимой переменной формируется правило, которое классифицирует объекты из обучающей выборки. При этом в заключительной части правила указывается значение зависимой переменной, которое наиболее часто встречается у объектов с выбранным значением независимой переменной. В этом случае ошибкой правила является количество объектов, имеющих то же значение рассматриваемой переменной, но не относящихся к выбранному классу. Таким образом, для каждой переменной будет получен набор правил (для каждого значения). Оценив степень ошибки каждого набора, выбирается переменная, для которой построены правила с наименьшей ошибкой.

Метод Naive Bayes

Алгоритм требуется для формирования элементарных правил для классификации объекта. Он строит правила по значению нескольких независимых переменных, используя формулу Байеса для расчета вероятности.

Вероятность того, что некоторый объект $i_j$ относится к классу $c_r$ (т.е. $y = c_r$, обозначим как $P(y = c_r)$. Событие, соответствующее равенству независимых переменных определенным значениям, обозначим как $E$, а вероятность его наступления $P(E)$. Идея алгоритма заключается в расчете условной вероятности принадлежности объекта к $c_r$ при равенстве его независимых переменных определенным значениям:

если $x_1 = c_p^1$ и $x_2 = c_d^2$ и $...$ и $x_m = c_b^m$, тогда $y = c_r$,

$P(y = c_r | E) = P(E | y = c_r) * \frac{P(y = c_r)}{P(E)}$

Для каждого из правил по формуле Байеса определяется его вероятность. Предполагая, что независимые переменные принимают значения независимо друг от друга:

$P(y = c_r | E) = P(x_1 = c_p^1 | y = c_r) * ... * P(x_m = c_b^m | y = c_r) * \frac{P(y = c_r)}{P(E)}$

$P(x_k = c_p^k | y = c_r) = \frac{P(x_k = c_p^k and y = c_r)}{P(y = c_r)}$

Методика "разделяй и властвуй"

Методика основана на рекурсивном разбиении множества объектов из обучающей выборки на подмножества, содержащие объекты, относящиеся к одинаковым классам. Сперва выбирается независимая переменная, которая помещается в корень дерева. Из вершины строятся ветви, соответствующие всем возможным значениям выбранной независимой переменной. Множество объектов из обучающей выборки разбивается на несколько подмножеств в соответствии со значением выбранной независимой переменной. Таким образом, в каждом подмножестве будут находиться объекты, у которых значение выбранной независимой переменной будет одно и то же. Относительно обучающей выборки T и множества классов C возможны три ситуации:

1. Множество $T$ содержит один или более объектов, относящихся к одному классу $c_r$. Тогда дерево решений для $T$ - это лист, определяющий класс $c_r$;множество $T$ не содержит ни одного объекта (пустое множество). Тогда это снова лист, и класс, ассоциированный с листом, выбирается из другого множества, отличного от $T$, например из множества, ассоциированного с родителем;
2. Множество $T$ содержит объекты, относящиеся к разным классам. В этом случае следует разбить множество $T$ на некоторые подмножества. Для этого выбирается одна из независимых переменных x_h, имеющая два и более отличных друг от друга значений $c_h^1, c_h^2, ..., c_h^n$;
3. Множество $T$ разбивается на подмножества $T_1, T_2,...,T_n$, где каждое подмножество $T_i$ содержит все объекты, у которых значение выбранной зависимой переменной равно $c_h^i$. Далее процесс продолжается рекурсивно для каждого подмножества до тех пор, пока значение зависимой переменной во вновь образованном подмножестве не будет одинаковым (когда объекты принадлежат одному классу). В этом случае процесс для данной ветви дерева прекращается.

Алгоритм покрытий

Алгоритм заключается в построении деревьев решений для каждого класса по отдельности. На каждом этапе генерируется проверка узла дерева, который покрывает несколько объектов обучающей выборки. На каждом шаге алгоритма выбирается значение переменной, которое разделяет множество на два подмножества. Разделение должно выполняться так, чтобы все объекты класса, для которого строится дерево, принадлежали одному подмножеству. Такое разбиение производится до тех пор, пока не будет построено подмножество, содержащее только объекты одного класса. Для выбора независимой переменной и её значения, которое разделяет множество, выполняются следующие действия:

1. Из построенного на предыдущем этапе подмножества (для первого этапа это вся обучающая выборка), включающего объекты, относящиеся к выбранному классу для каждой независимой переменной, выбираются все значения, встречающиеся в этом подмножестве.
2. Для каждого значения каждой переменной подсчитывается количество объектов, удовлетворяющих этому условию и относящихся к выбранному классу. Выбираются условия, покрывающие наибольшее количество объектов выбранного класса.
3. Выбранное условие является условием разбиения подмножества на два новых.

Мметод наименьших квадратов

Для $y = w_0 + w_1 * x_1 + ... + w_n * x_n = w_0 + \sum_{j = 1}^{n} w_j * x_j$

Задача заключается в отыскании таких коэффициентов w, чтобы удовлетворить условие:

$min R(f) = min \frac{1}{m} \sum_{l=1}^{m} (y_l - \sum_{i=1}^{n} w_l*f_l(x_i))$

Нелинейные методы

В простейшем случаем построение таких функций сводится к построению линейных моделей, для этого исходное пространство объектов преобразуется к новому

Support Vector Machines (SVM)

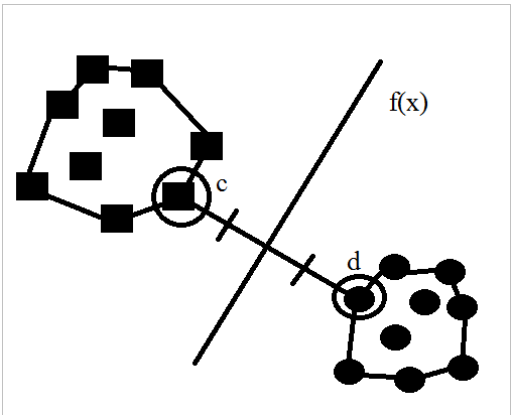
Для линейной функции идея метода основывается на предположении о том, что наилучшим способом разделения точек в m-мерном пространстве является m-1 плоскость (заданная функцией), равноудаленная от точек, принадлежащих разным классам.

Карты Кохонена

Самоорганизующаяся карта состоит из компонентов, называемых узлами или нейронами. Их количество задаётся аналитиком. Каждый из узлов описывается двумя векторами. Первый — т. н. вектор веса $m$, имеющий такую же размерность, что и входные данные. Второй — вектор $r$, представляющий собой координаты узла на карте. Карта Кохонена визуально отображается с помощью ячеек прямоугольной или шестиугольной формы; последняя применяется чаще, поскольку в этом случае расстояния между центрами смежных ячеек одинаковы, что повышает корректность визуализации карты.

Изначально известна размерность входных данных, по ней некоторым образом строится первоначальный вариант карты. В процессе обучения векторы веса узлов приближаются к входным данным. Для каждого наблюдения (семпла) выбирается наиболее похожий по вектору веса узел, и значение его вектора веса приближается к наблюдению. Также к наблюдению приближаются векторы веса нескольких узлов, расположенных рядом, таким образом если в множестве входных данных два наблюдения были схожи, на карте им будут соответствовать близкие узлы. Циклический процесс обучения, перебирающий входные данные, заканчивается по достижении картой допустимой (заранее заданной аналитиком) погрешности, или по совершении заданного количества итераций. Таким образом, в результате обучения карта Кохонена классифицирует входные данные на кластеры и визуально отображает многомерные входные данные в двумерной плоскости, распределяя векторы близких признаков в соседние ячейки и раскрашивая их в зависимости от анализируемых параметров нейронов.

В результате работы алгоритма получаются следующие карты:

• карта входов нейронов — визуализирует внутреннюю структуру входных данных путём подстройки весов нейронов карты. Обычно используется несколько карт входов, каждая из которых отображает один из них и раскрашивается в зависимости от веса нейрона. На одной из карт определенным цветом обозначают область, в которую включаются приблизительно одинаковые входы для анализируемых примеров.
• карта выходов нейронов — визуализирует модель взаимного расположения входных примеров. Очерченные области на карте представляют собой кластеры, состоящие из нейронов со схожими значениями выходов.

• специальные карты — это карта кластеров, полученных в результате применения алгоритма самоорганизующейся карты Кохонена, а также другие карты, которые их характеризуют.

• Инициализация карты, то есть первоначальное задание векторов веса для узлов.

• Цикл:
  1. Выбор следующего наблюдения (вектора из множества входных данных).
  2. Нахождение для него лучшей единицы соответствия (best matching unit, BMU, или Winner) — узла на карте, вектор веса которого меньше всего отличается от наблюдения (в метрике, задаваемой аналитиком, чаще всего, евклидовой).
  3. Определение количества соседей BMU и обучение — изменение векторов веса BMU и его соседей с целью их приближения к наблюдению.
  4. Определение ошибки карты.